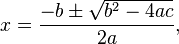
where x is the solutions of the quadratic equation: ax2+bx+c=0, a,b,c are real numbers, and a is non-zero.
Note: one should always indicate what all the symbols are within any formula.
Many high school Algebra 1 students freak out at this mildly ugly looking formula, didn't understand the derivation, and mumble in disgust while substitution the various a,b,c into their homework problems. Some even declare "I hate math" throughout their life after seeing this formula.
Recently I picked up a book discussing this formula (as introductory material to more interesting stuff). The author indicates that this formula is very old, dating back to the Bablyonians. A lot of information can be found on wiki.
Hmm, this makes me wonder, why is the formula old? A formula is timeless! It is there since day 1... It was discovered long ago that is. The Bablyonians were amazing. They didn't even have paper nor good math notations, yet they figured out LOTS of things and carved them on clay tablets.
To the "I hate math" folks, this formula is remarkable because it can tackle any quadratic equations, even those you can't factor. It also opens door to the imaginary world. If b2-4ac is negative, we require the imaginary number i to name a solution.
This formula can be fairly easily derived from the complete-the-square trick. It is a "real life application" that lets Algebra 1 students apply simple algebraic technique to derive a useful formula.
This formula can be used to derive the fascinating number: the golden ratio φ, which is the positive solution of the equation x2-x-1=0.
So, how many students get to use the quadratic formula after Algebra 1? I suppose not many. How many students need to know Columbus discovered America in 1492? (Ok, don't start a debate saying the Vikings or the Chinese did it first). The quadratic formula is a neat piece of knowledge and a problem solving tool.
No comments:
Post a Comment